Strona główna » ZA » Research »
Computational modeling of human blood circulation
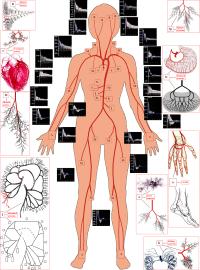
Blood flow and pulse wave propagation in arterial vasculatures are determined by their geometry, wall properties and wave reflection conditions. Important diagnostic information on the state of inner organs and whole body can be obtained by analysis of the pressure P(t) and flow U(t) or flow rate Q(t) curves measured in different arteries. Due to significant individual variations the influence of geometry of the vasculature and pathological conditions has to be separated for the correct analysis of the curves. Nowadays contemporary hemodynamics become rather computational science and mathematical models of different scale and dimensions are used for correct analysis of the blood circulation problems, modelling of pathologies, and planning of the therapeutic, surgery and rehabilitation procedures.
Multidimensional modeling of vascular systems
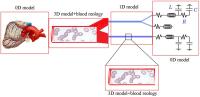
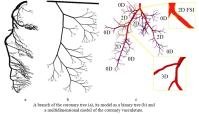
The multidimensional models are based on combination of 3D, 2D, 1D and 0D models for the blood vessels of different size and mechanical properties. For instance, the larger arteries can be recognized from the CT images and restored as 3D geometry. The larger arteries in the coronary vasculature are located over the heart surface (epicardium) and clearly visible on the angiographic images, MRI and CT images. Direct numerical computations on the 3D model of the system of ~6-12 epicardial arteries can be carried out when the total region is of interest for detailed computational data on the pressure and flow distributions, WSS and pressure oscillations, for instance, in the case of serial or bifurcation lesions, multivessel coronary disease. Otherwise the recognized geometry can be modeled as branching system of axisymmetric tubes (2D model) or system of compliant tubes with arbitrary cross-sectional geometry (1D model). The terminal vasculatures can be modeled basing on 2D, 1D or 0D models. Geometry of those vasculatures can be taken from the morphometric measurements or generated basing on the known geometric regularities.
The most of the multidimensional models presented in literature are based on combination of 3D, 1D and 0D models, that allows reduced order computations on the nonlinear model. As it was showed in numerous experiments on the coronary vessels and direct measurements, the larger and smaller coronary arteries exhibit high rigidity, small amplitude oscillations of their diameters and almost linear behaviour at physiological pressures. Therefore, it is reasonable to use linearized 2D model instead of non-linear 1D model that makes computations faster. The proposed here multidimensional model is based on combination of 3D, 2D and 0D models of the blood flow in the larger epicardial, smaller myocardial vessels and the microcirculatory system accordingly.
Geometrical parameters of human systemic arteriel tree have been measured on cadavers (5 sets of ~1000 arerial segments) and healthy volunteers (10 sets of ~100 arteries), while the intraorgan vasculatures have been srydied on the corrosion casts. The software for visualization of the arterial beds with given sets of diameters, lengths and numbers of the ends of the segments has been elaborated. Womersley model of the periodical blood flow and axisymmetric wave propagation in the anisotropic viscoelastic tubes have been used for detailed calculations of the flow rate Q(t) and pressure P(t) waves in the system. Validation of the model has been carried out by comparative study with the Q(t) and P(t) curves measured by Doppler ultrasound.
The 3D patient-specific model can be restored from the CT scans of the epicardial arteries of given patient. The CT scans are usually obtained at the end of diastole when the heart is relaxed and the coronary vessels are fully dilated. Branching geometry of the smaller myocardial vessels is generated basing on the statistical relations obtained from the measurements on the plastic casts of human coronary vasculatures that also correspond to their maximal vasodilatation. The areas of interest like stenoses, tortuous, irregular or branching paths can be embedded into the 2D trees as local 3D regions. The microcirculation is modelled as two element Windkessel providing quasi-stationary blood flow in the capillaries with variable resistivity and capacity.
Literature
1. Romashov Yu., Kizilova N., Gaidulis G. Mathematical Modeling of Mitral Valve Dynamics: Nonlinear vs Linear Models. Proc. of the 5th Intern. Conf. on Nonlinear Dynamics, Kharkov, Ukraine. – 2016. – P. 208-215.
2. Solovyova H., Kizilova N., Mizerski J. Nonlinear model of blood flow through stenosed coronary arteries. Proc. of the 5th Intern. Conf. on Nonlinear Dynamics, Kharkov, Ukraine. – 2016. – P. 384-389.
3. Kizilova N. Three chamber model of human vascular system for explanation the quasi-regular and chaotic dynamics of the blood pressure and flow oscillations. Applied Non-Linear Dynamical Systems. Jan Awrejcewicz (ed). Springer Proceedings in Mathematics & Statistics, Vol. 181. – 2016. - P. 209-220.
4. Kizilova N. Diagnostics of Coronary Stenosis: Analysis of Arterial Blood Pressure and Mathematical Modeling. Biomedical Engineering Systems and Technologies. Springer Series on Communications in Computer and Information Science. Plantier, G., Schulz, T., Fred, A., Gamboa, H. (Eds.) - 2015. - P.299-312.
5. Kizilova N. Patient-specific multidimensional model of coronary vasculature. Mechanika w Medycynie. Vol.12. Rzeszow Univ.Press. – 2014. – P. 108-119.
6. Kizilova N. Diagnostics of Coronary Stenoses - Analysis of Arterial Blood Pressure Signals and Mathematical Modeling. In: Proceedings of the International Conference on Bio-inspired Systems and Signal Processing. - 2014. - P.76-83.
7. Kizilova N., Philippova H., Zenin O. A realistic model of human arterial system: blood flow distribution, pulse wave propagation and modeling of pathology. Mechanics in Medicine. vol.10. Korzynskiego M., Cwanka J. (eds). Rzeszow. - 2010. – P.103-118.
8. Kizilova N. A 1000-tube model of human systemic arterial vasculature. Euromech Fluid Mechanics Conf. EFMC-9. Book of abstracts. – 2010. – S11-3.
9. Kizilova N., Hamadiche M., Gad-el-Hak M. Flow in Compliant Tubes: Control and Stabilization by Multilayered Coatings. Intern. J. Flow Control. - 2009. - v.1,N3. - P.199-211.
10. Hamadiche M., Kizilova N., Gad-el-Hak M. Suppression of Absolute Instabilities in the Flow inside a Compliant Tube. Communications in Numerical Methods in Engineering. 2009. vol.25,N5. P.505-531.
11. Zenin O.K., Kizilova N.N., Philippova E.N. Studies on the Structure of Human Coronary Vasculature. Biophysics. – 2007. - Vol. 52, No. 5. - P.499–503.
12. Kizilova N.N. Modeling of Intraorgan Arterial Vasculature. II. Propagation of Pressure Waves. Biophysics. – 2007. vol.52, N1. - pp.77–82.
13. Kizilova N.N. Modeling of intraorgan arterial vasculatures. I. A stationary blood flow at low Reynolds numbers. Biophysics. – 2006. v.51,N4. – P. 733-737.
14. Kizilova N.N. Investigation of Pressure - Flow Relations and the Parameters of the Forward and Backward Pressure Waves in Arterial Beds Intern.J.Fluid.Mech.Res. – 2006. - vol.33,N6. – P.537-552.
15. Kizilova N.N. Pressure wave propagation in liquid-filled tubes of viscoelastic material. Fluid Dynamics. - 2006. - v.41,N3. – P.434-446.
16. Kizilova N.N. Hydraulic Properties of Branching Pipelines with Permeable Walls. Intern. J. Fluid Mech.Res. – 2005. – vol.32,N1. – p.98-109.Kizilova N. A Detailed Digital Model of the Human Arterial System. Proc. of the 1-st Intern. Conf. on Complex Medical Engineering. Japan. – 2005. - P.287-292.
17. Kizilova N. A Detailed Digital Model of the Human Arterial System. Proc. of the 1-st Intern. Conf. on Complex Medical Engineering. Japan. – 2005. - P.287-292.
18. Kizilova N.N. Wave propagation and reflection in systems of compliant tubes. Intern. J. Fluid Mech.Res. – 2004. – vol.31,N6. – p.608-620.
19. Kizilova N.N. Computational approach to optimal transport network construction in biomechanics Lecture Notes in Computer Science. – 2004. - Vol.3044. – P.476-485. DOI: 10.1007/978-3-540-24709-8_51
20. Kizilova N.N. Рulse wave reflections in branching arterial networks and pulse diagnosis methods J.Chinese Inst. оf Engineers. – 2003. V.26 No.6. p.869-880. DOI: 02533839.2003.9670842