Hydrodynamic Instabilities

People:

Nikesh Yadav

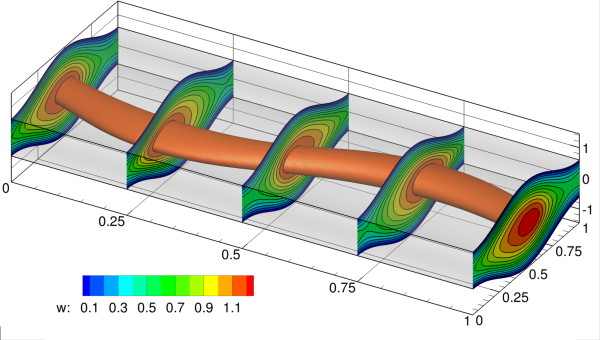
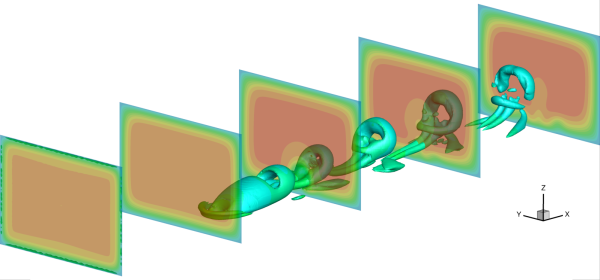
Some Colorful Fluid Dynamics:

High velocity tube resulting flow through a corrugated channel. The meandering of the tube has a form of a wave traveling downstream with the flow.

Jet in a crossflow. Isocontours of the Q-criterion illustrating vortical structures forming as a result of interaction of the jet and the crossflow. Hairpin vortices are apparent.

Publications:

• Yadav, N., S. W. Gepner, and J. Szumbarski (2017). Instability in a channel with grooves parallel to the flow. Physics of Fluids 29(8), 084104. eprint: http://dx.doi.org/10.1063/1.4997950.
• Gepner, S. W. and J. M. Floryan (2016). Flow dynamics and enhanced mixing in a converging–diverging channel. Journal of Fluid Mechanics 807, 167–204
• Szumbarski J., Blonski St., Kowalewski T.A.: Impact of Transversely-Orented Wall Corrugation on Hydraulic Resistance of a Channel Flow. The Archive of Mechanical Engineering, Vol. LVIII, No. 4, pp. 441-466, 2011.
• Szumbarski J., Blonski St.: Destabilization of a Laminar Flow in a Rectangular Channel by Transversely-Oriented Wall Corrugation. Archives of Mechanics, Vol. 63, No. 3, pp. 393-428, 2011.
• Husain S.Z., Floryan J.M., Szumbarski J.: Over-determined formulation of the immersed boundary conditions method. Computer Methods in Applied Mechanics and Engineering, 199, pp. 94-112, 2009.
• Kowalewski T.A., Szumbarski J.J., Błoński S.: Low-Reynolds-number instability of the laminar flow between wavy walls, Proceedings of the 6th International ASME Conference on Nanochannels, Microchannels and Minichannels, ICNMM2008-62070, June 23-25, 2008, Darmstadt, Germany. Publikacja w formie elektronicznej (8 stron).ISBN: 0-7918-4834-5
• Szumbarski J.: Instability of Viscous Incompressible Flow in a Channel with Transversely Corrugated Walls. Journal of Theoretical and Applied Mechanics, 45, 3, pp. 659-683, 2007.Szumbarski J., Floryan J.M.: Transient Disturbance Growth in a Corrugated Channel. Journal of Fluid Mechanics 568, pp. 243-272, 2006.
• Szumbarski J.J., Floryan J.M.: Channel Flow Instability in Presence of Weak Distributed Surface Suction. AIAA Journal, Vol. 28 No 2, pp.372-374, 2000.
• Cabal A., Szumbarski J., Floryan J.M.: Numerical simulation of flows over corrugated walls. Computers & Fluids 30, pp. 753-776, 2001.
• Szumbarski J., Floryan J.M.: A Direct Spectral Method for Determination of Flows over Corrugated Boundaries. Journal of Computational Physics 153, pp. 378-402, 1999.
• Szumbarski J., Immersed boundary approach to stability for a spatially periodic viscous flow. Archives of Mechanics, 54, 3, pp. 199-222, 2002.
• Cabal A., Szumbarski J., Floryan J.M., Stability of flow in a wavy channel. Journal of Fluid Mechanics, vol. 457, pp. 191-212, 2002.Szumbarski J., On Origin of Unstable Modes in Viscous Channel Flow Subject to Periodically  Distributed Surface Suction. Journal of Theoretical and Applied Mechanics, 40, 4, pp. 847-871, 2002.Floryan J.M., Szumbarski J., Wu X., Stability of flow in a channel with vibrating walls. Physics of Fluids, vol. 14, 11, pp. 3927-3936, 2002.